Panel data from cross-sectional DAGs

Create cross-sectional DAG

Declare variables.

z <- v("z", .f = d(~ rnorm(n = 10^3, mean =  rsum(.x), sd = 1)))
x <- v("x", .f = d(~ rnorm(n = 10^3, mean =  rsum(.x), sd = 1)))
y <- v("y", .f = d(~ rnorm(n = 10^3, mean =  rsum(.x), sd = 1)))

Declare causal relations.

g <- (z * b(1) + x * b(1)) * y +
     (z * b(1) * x)
plot(g)

Create time series structure

Declare periods.

t1 <- v("t1", .f = d(~ rnorm(n = 10^3, mean = rsum(.x), sd =  1)))
t2 <- v("t2", .f = d(~ rnorm(n = 10^3, mean = rsum(.x), sd =  1)))
t3 <- v("t3", .f = d(~ rnorm(n = 10^3, mean = rsum(.x), sd =  1)))
t4 <- v("t4", .f = d(~ rnorm(n = 10^3, mean = rsum(.x), sd =  1)))
t5 <- v("t5", .f = d(~ rnorm(n = 10^3, mean = rsum(.x), sd =  1)))

Specify persistence.

t <- (t1 * b(1) * t2) + (t2 * b(1) * t3) +
     (t3 * b(1) * t4) + (t4 * b(1) * t5)

plot(t)

Take product of cross section and timeseries

Combine cross-sectional and time series DAGs.

xt <- cartesian_product(g,t,node_combine =  ~ c(.x), edge_combine =  ~ c(.x,.y))
plot(xt)

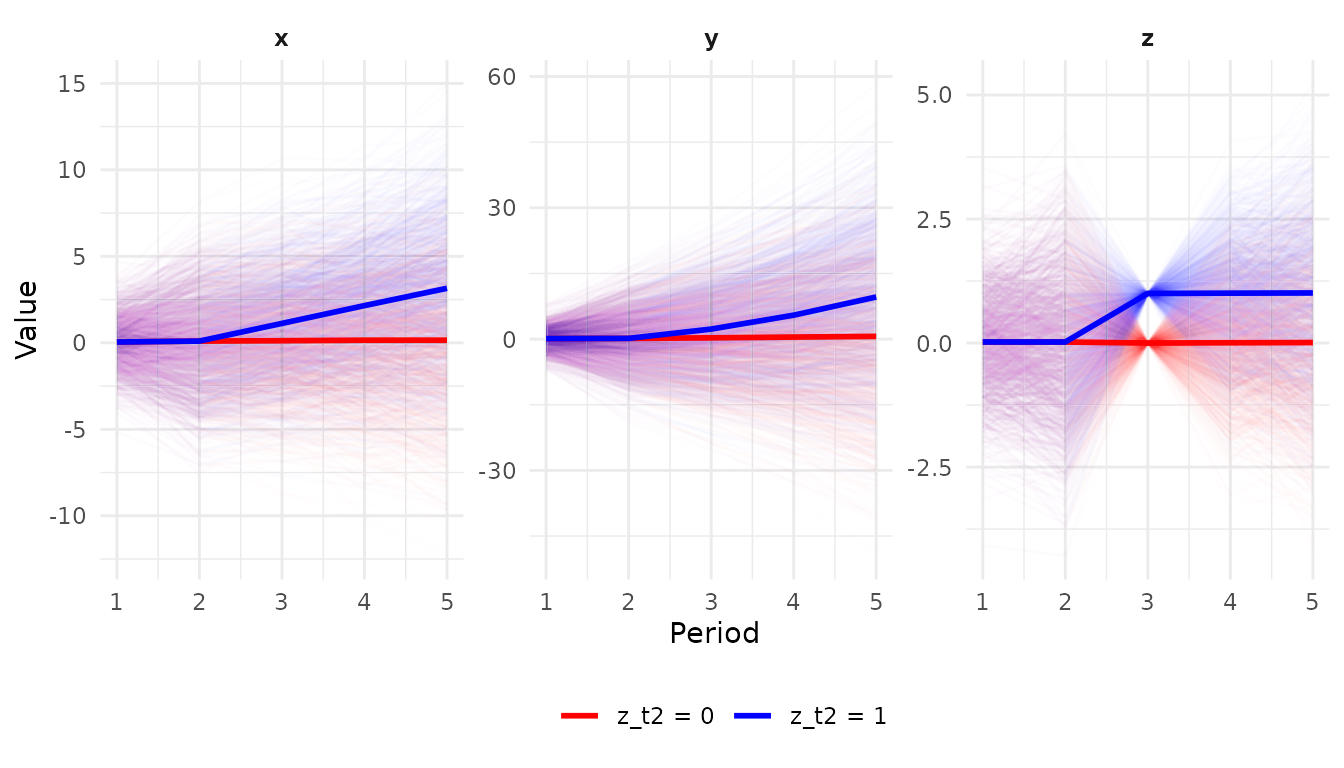
Compare intervention outcomes

Compare \(E(Y|do(z_{t3}=0)\) with \(E(Y|do(z_{t3}=1)\).

z_t2_0 <- xt %>% manipulate(z_t3 = 0) %>% simulate(label = "z_t2 = 0",seed = 2)
z_t2_1 <- xt %>% manipulate(z_t3 = 1) %>% simulate(label = "z_t2 = 1",seed = 2)

bind_rows(z_t2_0,z_t2_1) %>% panel_gather() %>% panel_plot()